A moment 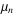 of a univariate probability
function of a univariate probability
function 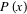 taken about the mean taken about the mean 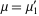 , ,
where 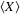 denotes the expectation
value. The central moments denotes the expectation
value. The central moments 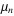 can be expressed as terms of the raw moments can be expressed as terms of the raw moments
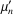 (i.e., those taken about zero) using the binomial
transform (i.e., those taken about zero) using the binomial
transform
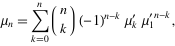 |
(3) |
with 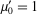 (Papoulis 1984, p. 146). The first few
central moments expressed in terms of the raw moments
are therefore (Papoulis 1984, p. 146). The first few
central moments expressed in terms of the raw moments
are therefore
These transformations can be obtained using
CentralToRaw[n] in the Mathematica
application package mathStatica.
The central moments 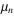 can also be expressed in terms of the cumulants can also be expressed in terms of the cumulants 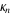 , with the first few cases given by , with the first few cases given by
These transformations can be obtained using
CentralToCumulant[n] in the Mathematica
application package mathStatica.
The central moment of a multivariate probability
function 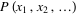 can be similarly defined as can be similarly defined as
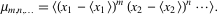 |
(13)
|
Therefore,
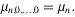 |
(14)
|
For example,
Similarly, the multivariate central moments can be
expressed in terms of the multivariate cumulants. For example,
These transformations can be obtained using
CentralToRaw[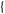 m, n, ... m, n, ...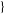 ] in the Mathematica
application package mathStatica
and CentralToCumulant[ ] in the Mathematica
application package mathStatica
and CentralToCumulant[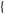 m, n, ... m, n, ...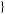 ], respectively. ], respectively.

Kendall, M. G. "The Derivation of
Multivariate Sampling Formulae from Univariate Formulae by Symbolic
Operation." Ann. Eugenics 10, 392-402, 1940.
Kenney, J. F. and Keeping, E. S.
"Moments About the Mean." §7.3 in Mathematics
of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van
Nostrand, pp. 92-93, 1962.
Papoulis, A. Probability,
Random Variables, and Stochastic Processes, 2nd ed. New
York: McGraw-Hill, p. 146, 1984.
Smith, P. J. "A Recursive Formulation of the
Old Problem of Obtaining Moments from Cumulants and Vice Versa."
Amer. Stat. 49, 217-218, 1995.
|